Geometria
Descartes's "application of modern algebraic arithmetic to ancient geometry created the analytical geometry which is the basis of the post-Euclidean development of that science" -Printing and the Mind of Man
“Probably the most important of all his legacies to science, for in its pages is to be found the exposition of a new science, the science of coordinate geometry” -Scott, Scientific Work of Descartes
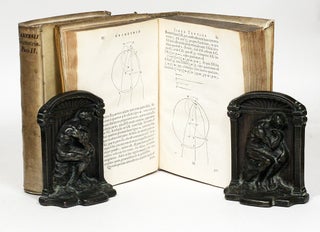
RARE 1659-1661 SECOND EDITION OF DESCARTES’S GEOMETRY, GREATLY EXPANDED FROM THE 1649 FIRST EDITION BY THE ADDITION OF IMPORTANT COMMENTARY: "This edition served as the basic textbook for the generation that, in the last quarter of the century, took the lead in introducing differential and integral calculus" (Jahnke). A beautiful copy in contemporary vellum.
On November 10, 1619, "the most important event of Descartes's life occurred... Descartes spent the whole day snugly tucked up in bed, dreaming (or daydreaming) about the nature of the world... [and] it was on this day that Descartes first saw the road to his own philosophy and also had one of the greatest mathematical insights of all time.
"Idly watching a fly buzzing around in the corner of the room, Descartes suddenly realized that the position of the fly at any moment in time could be represented by three numbers, giving its distance from each of the three walls that met in the corner. Although he instantly saw this in three-dimensional terms, the nature of his insight is now known to every schoolchild who has ever drawn a graph. Any point on the graph is represented by two numbers, corresponding to the distances along the x axis and up the y axis. In three dimensions, you just have a z axis as well. The numbers used in the system of representing points in space (or on a piece of paper) in this way are now known as Cartesian co-ordinates, after Descartes... Descartes's discovery meant that any geometric shape could be represented simply by a set of numbers... And any curved line drawn on paper (or, for example, the orbit of a planet around the Sun) could also be represented, in principle, by a series of numbers related to one another by a mathematical equation. When this discovery was fully worked out and eventually published, it transformed mathematics by making geometry susceptible to analysis using algebra, with repercussions that echo right down to the development of the theory of relativity and quantum theory in the twentieth century. Along the way, it was Descartes who introduced the convention of using letters at the beginning of the alphabet (a,b,c ...) to represent known (or specified) quantities, and letters at the end of the alphabet (especially x,y,z) to represent unknown quantities. And it was he who introduced the now familiar exponential notation... If he had done nothing else, laying all these foundations of analytical mathematics would have made Descartes a key figure in seventeenth-century science" (Gribben, The Scientists).
On the history and importance of the second edition:
"Within a few years of its publication, Descartes' La geometrie, originally written as an appendix to his Discours, was translated into Latin by Frans van Schooten and republished in its own right under the title Geometria in 1649. Ten years later van Schooten brought out a second edition, now expanded to two volumes by the commentary and research that had already accumulated around Descartes' text, much of it from van Schooten himself or from his pupils, such as Jan Hudde and Hendrik van Heuraet. Four treatises in this second edition were particularly concerned with equations, two by Florimond de Beaune and two by Jan Hudde" (Stedall, From Cardano's Great Art to Lagrange's Reflections).
"In the second edition [of Geometria] (van Schooten 1659-1661), in two volumes, the commentaries were enlarged, and van Schooten included work by his students van Heuraet, Hudde, Huygens and de Witt. This edition served as the basic textbook for the generation that, in the last quarter of the century, took the lead in introducing differential and integral calculus" (Jahnke, A History of Analysis).
Complete with half-titles and frontispiece portrait to volume I. An exquisitely-printed book, illustrated throughout with in-text diagrams.
Geometria a Renato Des Cartes anno 1637 Gallice edita, postea autem una cum notis Florimondi de Beaune (...) in Latinam linguam versa & commentariis illustrata [ed. Franciscus van Schooten]. Amsterdam: L. & D. Elzevier, 1659 [Pt. 1] 1661 [Pt. 2]. Small quarto, contemporary full limp vellum. Two volumes. Text in Latin. Handsome ink stamp of the renowned 19th-century Parisian bookseller and publisher Ambroise Lefèvre (“Librairie Scientifique Ancienne & Moderne”) on preliminary blanks of each volume. A FINE COPY, with text nearly pristine.
Check Availability:
P: 212.326.8907
E: info@manhattanrarebooks.com